SKIN EFFECT IN SEMICONDUCTOR WIRES:
So far, we have considered the resistance of a semiconductor wire to be linear and constant. This is definitely the case for most semiconductor circuits. At very high frequencies however, an additional phenomenon called the skin effect comes into play such that the resistance becomes frequency-dependent.
High-frequency currents tend to flow primarily on the surface of a conductor with the current density falling off exponentially with depth into the conductor. The skin depth d is defined as the depth where the current falls off to a value of e -1 of its nominal value, and is given by
with f the frequency of the signal and U the permeability of the surrounding dielectric (typically equal to the permeability of free space, or m = 4p ´ 10-7 H/m). For Aluminum at 1 GHz, the skin depth is equal to 2.6 mm.
The obvious question is now if this is something we should be concerned about when designing state-of-the-art digital circuits?
The effect can be approximated by assuming that the current flows uniformly in an outer shell of the conductor with thickness d, as is illustrated in Figure for a rectangular wire. Assuming that the overall cross-section of the wire is now limited to approximately
we obtain the following expression for the resistance (per unit length) at high frequencies (f > fs):

The increased resistance at higher frequencies may cause an extra attenuation and hence distortion of the signal being transmitted over the wire. To determine the on-set of the skin-effect, we can find the frequency fs where the skin depth is equal to half the largest dimension (W or H) of the conductor. Below fs the whole wire is conducting current, and the resistance is equal to (constant) low-frequency resistance of the wire. From Eq. (4.6), we find the value of fs:



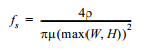
No comments:
Post a Comment